Capítulo 2 Inferência Estatística
Texto baseado no livro A Estatística Básica e sua Prática David S. Moore (2011)
Ao extrair uma amostra, sabemos exatamente todas as respostas dos entrevistados. Entretanto, não queremos somente isso. Queremos também construir conclusões sobre a população. Em outras palavras, queremos generalizar os resultados da amostra para a população. O processo para isso é chamado inferência estatística. De fato, o nosso unico interesse em uma amostra aleatória é que ela forneça informação que possa ser generalizada para a população maior.
A média da amostra não será exatamente igual à méda da população (evento muito raro. chance mínima disso acontecer). Se pudessemos extrair uma outra amostra da mesma população, os resultados dessa nova amostra poderia nos conduzir a conclusões diferentes. Como ter certeza que as conclusões baseadas em uma única amostra estão corretas? A inferencia estatística usa a linguagem da probabilidade para expressar o grau de confibilidade de nosas conclusões.
Assim, esperamos que a amostra forneça alguma informação sobre a média populacional, embora saibamos que não será livre de erros. isso pode ser representado como uma equação:
\[\bar{X}=\mu+\epsilon\]
Onde \(\bar{X}\) é a média amostral, \(\mu\) (a letra grega mi) é a média populacional e \(\epsilon\) é o erro amostral. Esse ultimo termo dfa equação pode assumir valores positivos e negativos (erro para mais ou para menos). O que essa equação está querendo dizer é:
Estatística Amostral = Parametro Populacional + Erro Amostral
As duas abordagens mais comuns da inferência estatística para isso são chamadas de:
- Intervalos de confiança
- Teste de Hipóteses
Ambos os tipos de inferência baseiam-se nas distribuições amostrais de estatísticas.
2.1 Distribuições Amostrais
Suponha que na cidade do Rio de Janeiro só temos cinco empresas, isto é, uma população de 5 unidades. Vamos imaginar que os lucros dessas empresas foram de 8, 9, 10, 11 e 12 unidades monetárias. É facil verificar que o parâmetro da população da média é igual a 10 unidades. Vamos representar esse parâmetro por uma letra grega. Em outras palavras, vamos considerar \[\mu=10\]. Além disso, o desvio padrão desses valores é \[ \sigma=1,41\].
empresa<-c(8,9,10,11,12)
mean(empresa)## [1] 10Dessa população-alvo de 05 elementos, quero extrair todas as possíveis amostras de 03 elementos, com reposição, conforme mostrado na tabela ao lado.
| Amostra_Extraida_tamanho_3 | Media_Amostra |
|---|---|
| 8,8,8 | 8.00 |
| 8,8,9 | 8.33 |
| 8,8,10 | 8.67 |
| 8,8,11 | 9.00 |
| 8,8,12 | 9.33 |
| 8,9,8 | 8.33 |
| 8,9,9 | 8.67 |
| 8,9,10 | 9.00 |
| 8,9,11 | 9.33 |
| 8,9,12 | 9.67 |
| Etc | NA |
Nessa tabela extraimos (com reposição) todas as amostras possíveis. A primeira amostra foi aquela onde sorteamos o lucro. a segunda amostra foi 8,8,9. Na segunda coluna temos a média dessas amostras sorteadas.
Interessante notar que a média da amostra igual a 8 é muito rara e só acontece uma unica vez. Isso só ocorre quando a amostra é igual a 8,8,8. Já a média da amostra igual a 8,33 ocorre em três situações:
- 8,8,9
- 8,9,8
- 9,8,8
Após calculado o valor de média é possível agrupar de acordo com o número de vezes que esses valores aparecem.
Nessas três situação a resultante será a média 8,33. Fazendo a frequência de todas as médias possíveis encontramos a seguinte tabela:
| Media | Frequencia |
|---|---|
| 8.00 | 1 |
| 8.33 | 3 |
| 8.67 | 6 |
| 9.00 | 10 |
| 9.33 | 15 |
| 9.67 | 18 |
| 10.00 | 19 |
| 10.33 | 18 |
| 10.67 | 15 |
| 11.00 | 10 |
| 11.33 | 6 |
| 11.67 | 3 |
| 12.00 | 1 |
Podemos fazer um gráfico da frequência das médias amostrais.
barplot(Distribuicao$Frequencia,col="#175d5e",xlab="Médias das Amostras",ylim=c(0,20))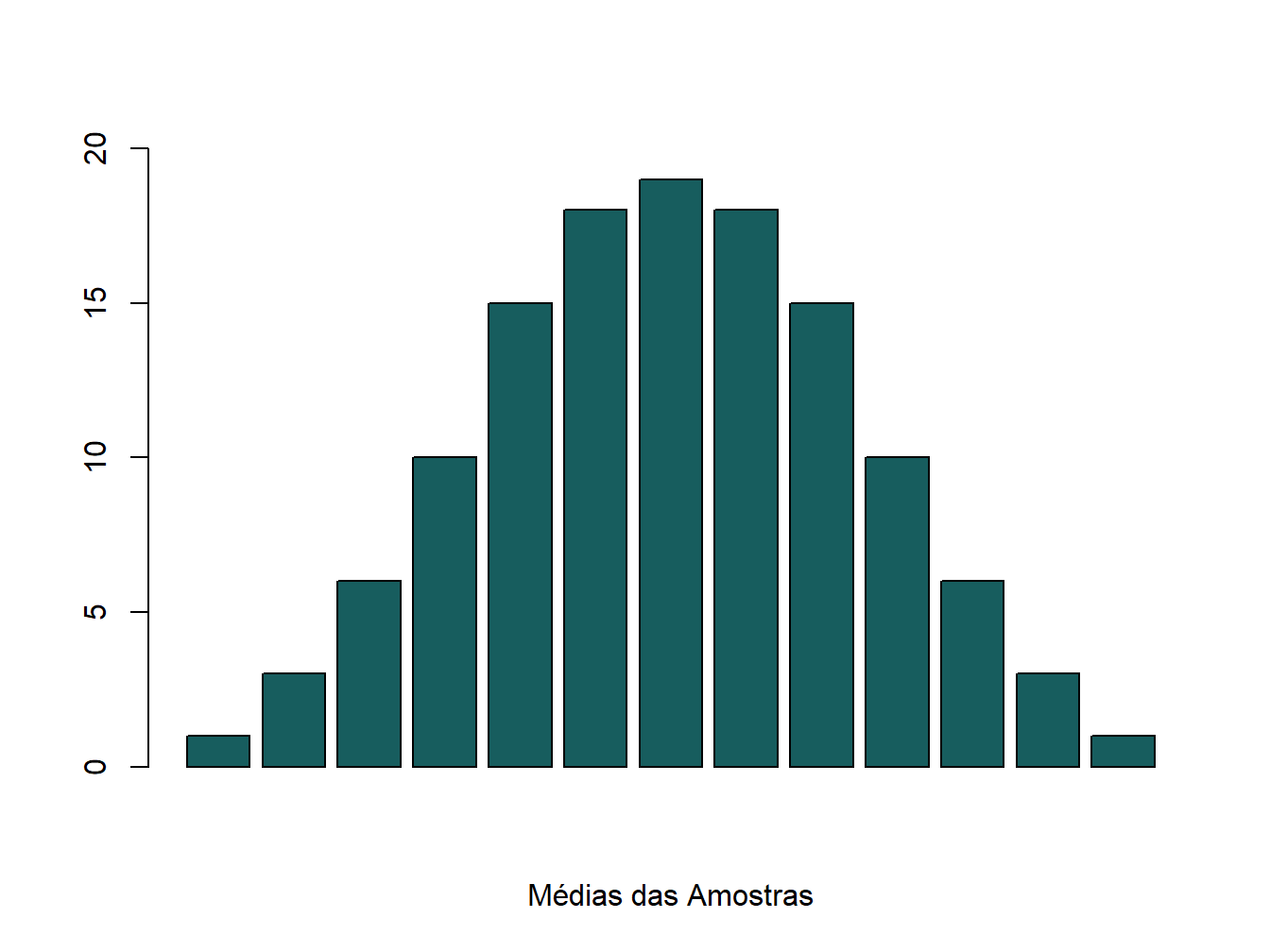
Figura 2.1: Distribuição das médias das amostras de três elementos
Esse gráfico é muito semelhante ao gráfico da distribuição normal. Tem um formato de sino, é simétrico, etc.
Outro fato interessante é que a média das médias amostrais é igual a 10 (parâmetro da média da população).
Além disso, supondo amostras com 03 elementos, com reposição. Será possível estabelecer 125 possíveis resultados. A média desses resultados será 10,00. O desvio padrão será 0,8185.
Considerando a distribuição Normal, se temos a média e o desvio padrão, podemos utilizar a regra empírica 68%, 95%, 99,7% para calcular probabilidades do relacionamento entre a média da amostra e a média da população.
2.2 Aplicação prática
Vamos utilizar um exemplo real. No pacote chamado TeachingSampling tem uma base de dados com 2.396 linhas chamada Lucy. O que queremos é extrair amostras aleatórias desse banco de dados de diversos tamanhos e calcular o valor de Income (renda) médio.
library(TeachingSampling)
data(Lucy)
dim(Lucy)## [1] 2396 8Vamos extrair uma Amostra Aleatória Simples (AAS) desse banco de dados. A amostra que vamos extrair será de tamanho igual a 400.
A função para fazer isso no R é S.WR(N,m).Esse nome vem de: Sampling With Replacement (N=Tamanho da população,m=Tamanho da Amostra)
N <- dim(Lucy)[1]
m <- 400
sam<-S.WR(N,m)
data <- Lucy[sam,]
dim(data)## [1] 400 8mean(Lucy$Income)## [1] 432.0605mean(data$Income)## [1] 422.4025A média da amostra não ficou próxima da média da população? E se extrairmos outra amostra? Recomendo fortemente que você faça isso. O valor da amostra fica algo entorno do verdadeiro valor da população, não? Isso porque os valores seguem uma distribuição Normal. O que quero dizer com isso? Que as amostras não são extraidas para acertar na mosca, mas sim para chegar bem perto do verdadeiro valor populacional. Podemos então pensar em um intervalo em 95% das vezes o verdadeiro valor estará incluido. Esse é o tema do proximo capítulo.
Desse modo, podemos errar para mais ou para menos. A média da amostra poder ser um pouco maior ou um pouco menor qie a média da população. Se extrairmos muitas amostras, cad auma terá um média, mas espéramos que elas difiram umas das outras e da média populacional por chance aleatória.
2.3 Exercício
- Gerar uma população de tamanho 100.000 com média igual a 100 e desvio padrão igual a 20
- Gerar uma amostra de tamanho 100
- Calcular a média da população
- Calcular a média da amostra
- Ver a diferença entre a média da amostra e a média da população
- repetir os passos 2 a 6 pelo menos cinco vezes
# Definindo o tamanho da população e da amostra
N <- 100000
m <- 100
# Gerando uma conjunto de dados (Populacao)
Populacao<- data.frame(rnorm(N, 100, 20))
# Gerando uma amostra
sam<-S.WR(N,m)
amostra <- data.frame(Populacao[sam,])
# Comparando a distribuicao da amostra com a da populacao
summary(amostra)## Populacao.sam...
## Min. : 45.06
## 1st Qu.: 85.48
## Median : 98.12
## Mean : 99.86
## 3rd Qu.:111.23
## Max. :146.97summary(Populacao)## rnorm.N..100..20.
## Min. : 15.67
## 1st Qu.: 86.49
## Median :100.00
## Mean :100.01
## 3rd Qu.:113.52
## Max. :188.01Mais aplicações da relação da média da amostra com a média da população pode ser encontrada aqui